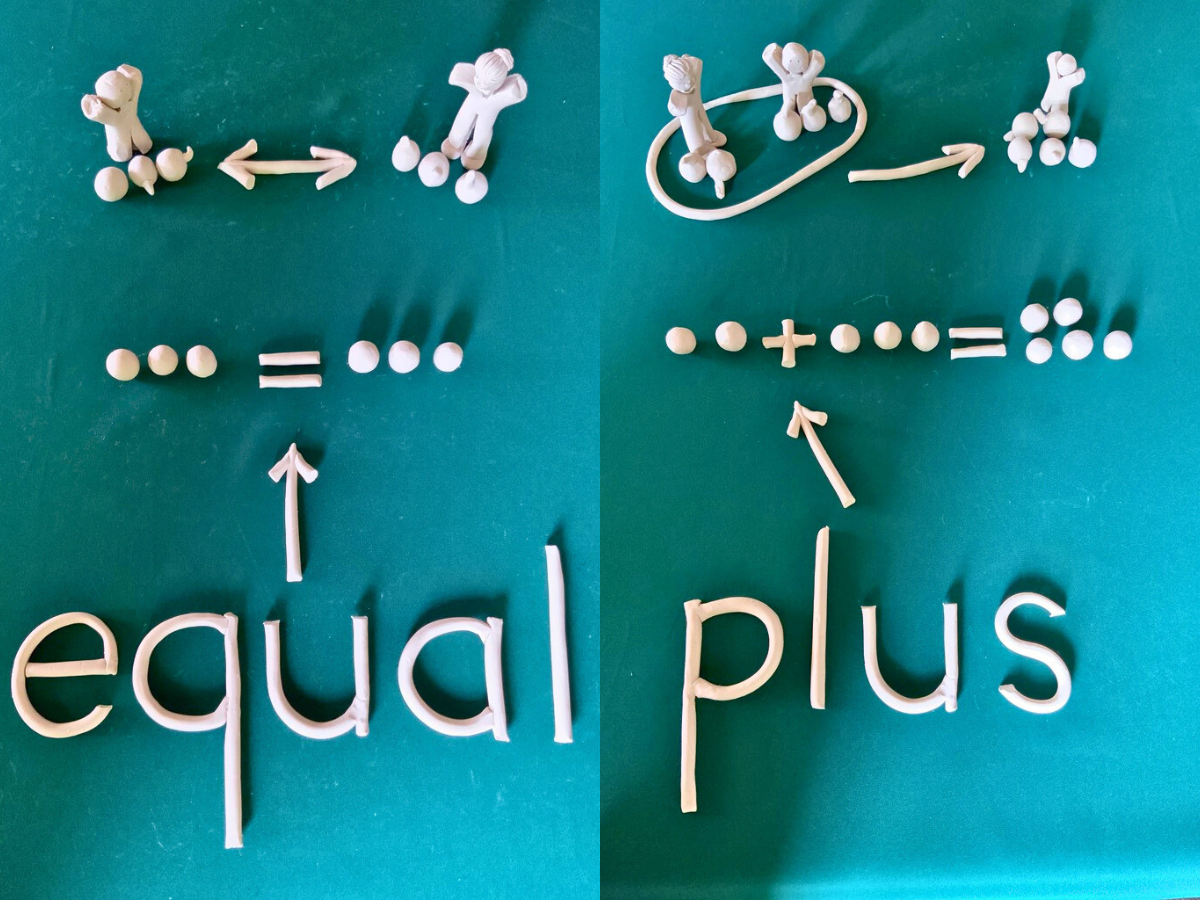
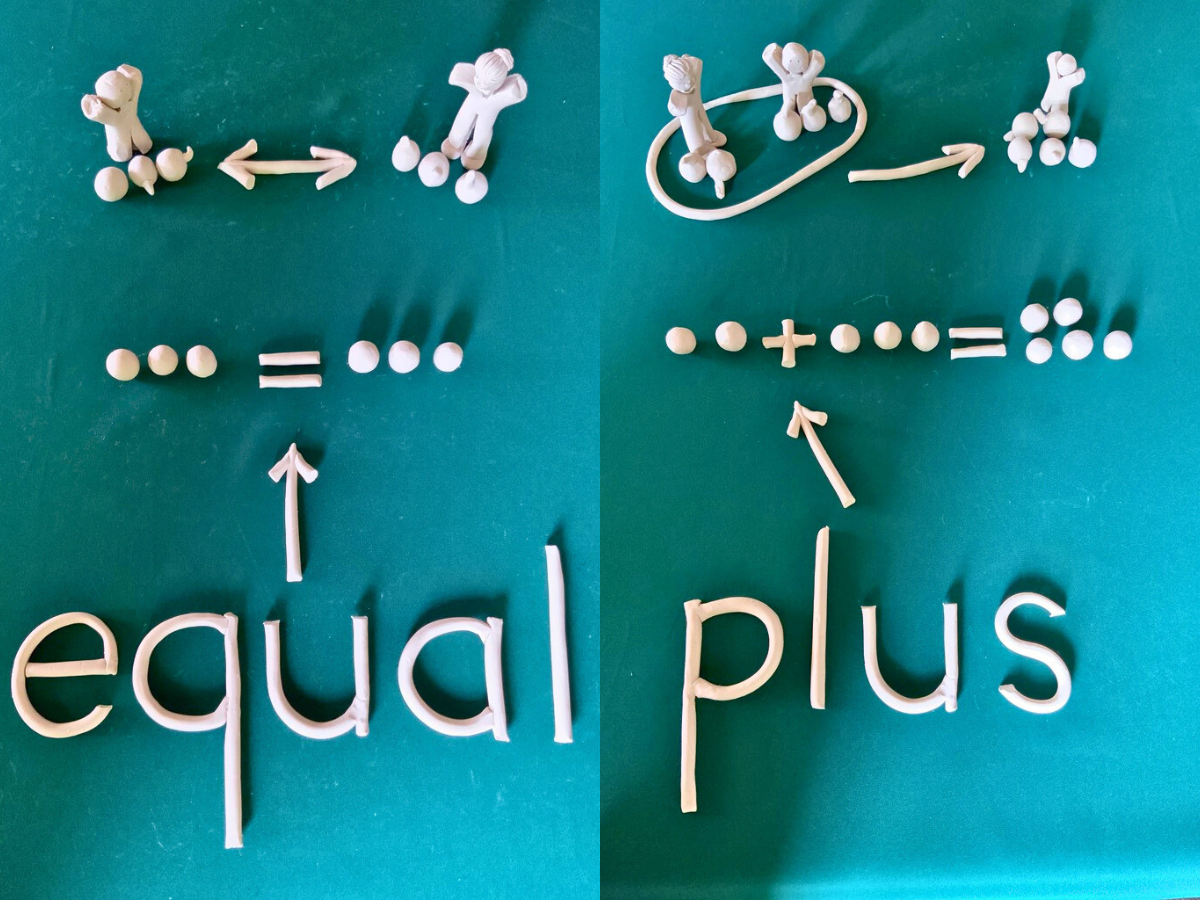
Math teachers routinely use multiple words for the same concept — add, plus, added to — switching between them naturally during lessons. But for dyslexic children, this seemingly simple language flexibility can create profound confusion.
A recent planning meeting with math teacher Geoffrey Ashiono highlighted this challenge and sparked a discussion about how Davis Method clay modeling can provide clarity where traditional teaching methods fall short.
Math teachers naturally use synonymous terms interchangeably:
While teachers understand these words mean the same thing, dyslexic children often don’t. When a teacher says “add” one minute, then “plus” the next, then “added to,” confusion sets in. Do they mean the same thing or different operations?
This uncertainty undermines mathematical confidence before calculations even begin.
Dyslexic learners are primarily picture-thinkers who benefit from concrete, visual representations. They need context and narrative to connect with learning — something that makes abstract concepts tangible and relatable.
Clay modeling provides exactly this foundation.
One 8-year-old learner came from a farm where they grew watermelons. The child loved watermelon, so his context for learning became watermelons. He also wanted to learn the meaning of “equal” — if his sister had three melons, he definitely wanted three melons too!
This personal connection became the foundation for understanding mathematical concepts.
First, establish the core concept:
Addition means “putting together” two or more quantities. When you add, you join something to something else so there is more. The “more” is crucial — it helps children realize the answer should always be bigger than the starting number.
Next, connect multiple terms to one meaning:
Using clay models, children learn that “add” has the same meaning as “plus” and that both connect to the + symbol. This gives certainty to children listening to mathematical language.
The child creates a visual representation using clay balls to represent quantities. For the equation 2 + 3 = 5:
Reading left to right: 2 plus 3 equals 5 Alternative reading: 3 added to 2 equals 5
Both phrasings use the same clay model and the same + symbol, making the connection clear.
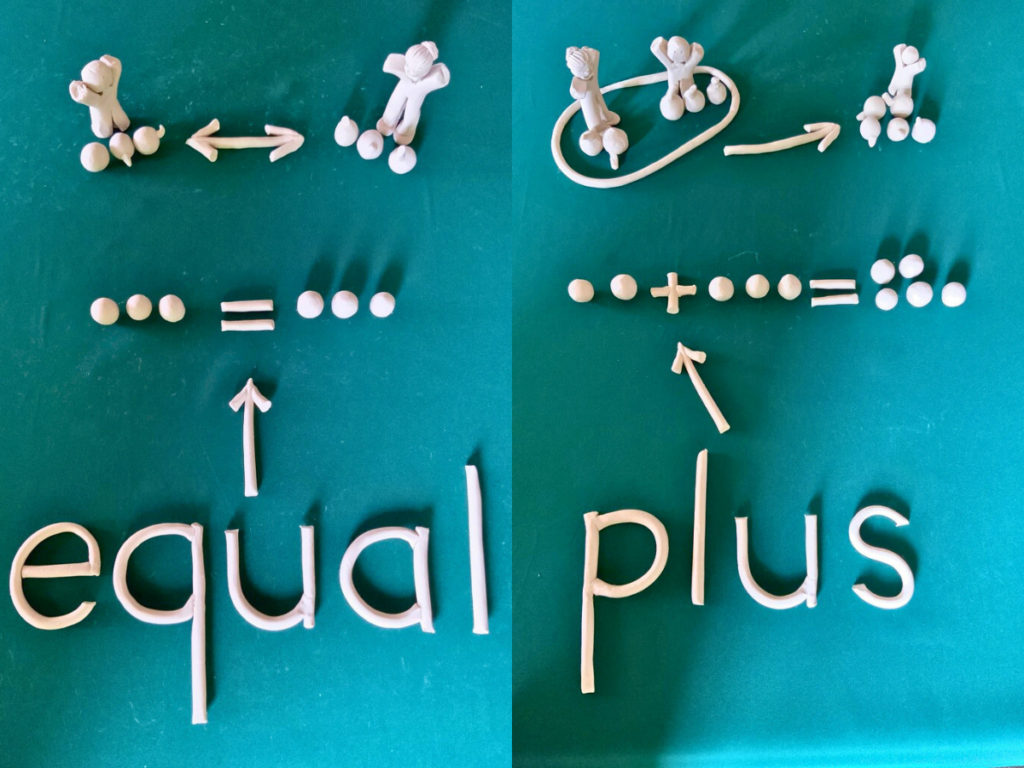
Mathematical symbols often confuse visual-spatial learners. Clay modeling addresses this by making abstract symbols concrete:
Where is the meaning of plus? → Point to the + sign Where is the meaning of add? → Point to the + sign
The physical model shows that different words point to the same symbol and concept.
After creating the model, the learner takes control. They guide others through a summary of their clay work, pointing at the model while explaining the meaning. This active teaching role reinforces understanding and builds confidence.
Picture-thinking learners need:
Clay modeling provides all these elements while addressing the specific challenge of mathematical language confusion.
This approach works for all mathematical operations. Whether working with subtraction (minus, take away), multiplication (times, by), or division (divide, share), clay models help dyslexic learners understand that multiple words can represent the same mathematical concept.
The key is providing concrete, visual anchors for abstract mathematical language.
When dyslexic children understand that mathematical terms are simply different names for the same operations, confusion decreases and confidence grows. They can focus on learning mathematics rather than decoding conflicting language.
This clarity becomes the foundation for mathematical success, allowing picture-thinking learners to engage with math using their natural strengths rather than struggling against language barriers.
Learn more about the Davis® Mastery for Dyslexia here, connect with Claire or find a Davis® Facilitator in your area.